跳到主要内容

理论基础

在 Uniswap v1/v2 使用的恒定乘积做市商公式中，对于给定价格，池子中仅部分资金参与做市。这显得十分低效，特别是当代币总是在特定价格附近交易时。

在 Uniswap v3 中提供了一种新颖的自动做市商（AMM）系统，它使流动性提供者(LP)能够更好地控制其资金使用的价格范围，并降低流动性分裂和 gas 消耗等问题的影响。Uniswap v3 基于与之前版本相同的常值函数曲线，提供了几个重要的新功能：

  • 集中流动性：流动性提供者（LP）将被赋予在任意价格区间提供流动性的能力。这将提高池子的资金利用率，并允许 LP 估算他们认可的价格曲线，一起提供高效聚合的流动性

  • 灵活的手续费：交换费不再锁定在 0.30%，相反，每个池子（每个交易对可能有多个）的费用层级在初始化时设置，默认支持的费用层级为 0.05%，0.30%和 1%。 通过 UNI 治理可以向该集合添加其他值。

  • 协议手续费治理：UNI 治理可以灵活设置协议手续费对交易手续费的分成占比

  • 改进的价格预言机: 为用户提供了一种方式查询近期累计价格，从而避免了在计算 TWAP（时间加权平均价格）的时间段开头和结尾手动记录累计价格。

  • 流动性预言机：合约提供了一种时间加权平均流动性的预言机

集中流动性​

在 v2 版本中流动性被均匀分布在曲线 x⋅y=kx \cdot y = k，导致资金利用率低。

为了提升资金利用，v3 允许 LP 将他们的流动性集中到指定的价格区间内。集中到一个有限区间的流动性被称为 头寸，一个头寸只需要维持足够的代币余额以支持该区间的交易即可。

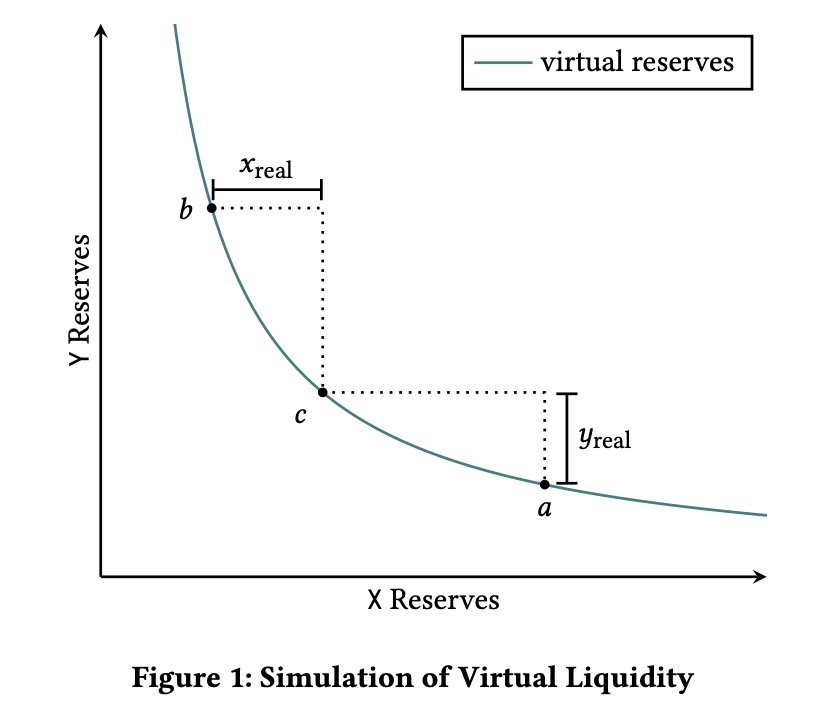
figure1

在图中 LP 只在 [a, b] 价格区间内提供流动性。价格则是指的相对价格。假设在流动池中的两个币种 token0 和 token1 的数量分别是 xx 和 yy，则 token0 相对于 token1 的价格就是 y/xy / x, token1 相对于 token0 的价格就是 x/yx / y

  • a 点 token0 的价格是 pa=yaxap_a = \frac{y_a}{x_a}
  • b 点 token0 的价格是 pb=ybxbp_b = \frac{y_b}{x_b}

由于只在[a, b] 区间内提供流动性，同时又为了使曲线满足 x⋅y=kx \cdot y = k, 因此引入了一个新的概念: 虚拟流动性。 因此在 [a, b] 区间内的所有点满足

(xreal+xvirtual)×(yreal+yvirtual)=k(x_{\tt{real}} + x_{\tt{virtual}}) \times (y_{\tt{real}} + y_{\tt{virtual}}) = k

其中 xrealx_{\tt{real}} 和 yrealy_{\tt{real}} 是用户真实提供的 token 数量，xvirtualx_{\tt{virtual}} 和 yvirtualy_{\tt{virtual}} 代表流动池虚拟出的 token 数量，为了能保证价格计算的一致性，并不参与实际的交易，而且只限于[a, b]这个区间，当价格超出[a, b]这个区间时，xvirtualx_{\tt{virtual}} 和 yvirtualy_{\tt{virtual}} 会被移除。

当曲线 x⋅y=kx \cdot y = k 平移至坐标轴， 即将曲线沿横坐标平移−xb-x_b, 沿纵坐标平移−yb-y_b，即可得到真实流动性储备量曲线

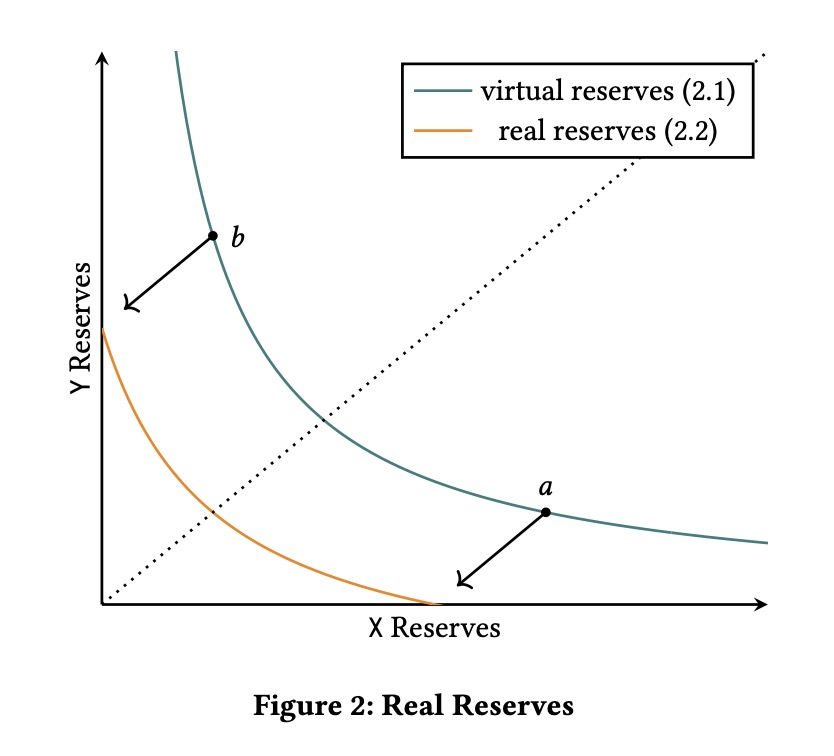
figure2

平移后的曲线为

(x+xb)×(y+ya)=k(x + x_b) \times (y + y_a) = k

在 Uniswap V2 中，流动性是通过流动性池的大小来衡量的。但在 V3 中，由于流动性提供者可以选择提供流动性的价格范围，所以不能简单地使用流动性池的大小来衡量流动性。为了解决这个问题，Uniswap V3 引入了一个新的概念，即流动性数量 L

L=k=xyL=\sqrt{k} = \sqrt{xy}

结合上式得到

pa=yaxaL2=xa⋅ya}⇒ya=Lpa\left. \begin{array}{r} p_a = \frac{y_a}{x_a} \\[1.5ex] L^2 = x_a \cdot y_a \end{array} \right\} \Rightarrow y_a = L\sqrt{p_a} pb=ybxbL2=xb⋅yb}⇒xb=Lpb\left. \begin{array}{r} p_b = \frac{y_b}{x_b} \\[1.5ex] L^2 = x_b \cdot y_b \end{array} \right\} \Rightarrow x_b = \frac{L}{\sqrt{p_b}}

代入公式

(x+xb)×(y+ya)=k(x + x_b) \times (y + y_a) = k

得到关于 LP 在价格区间 [a, b] 之间的流动性数量的公式

(x+Lpb)×(y+Lpa)=L2(x + \frac{L}{\sqrt{p_b}}) \times (y + L\sqrt{p_a}) = L^2

假设存在交易对 ETH-USDC 如下图所示

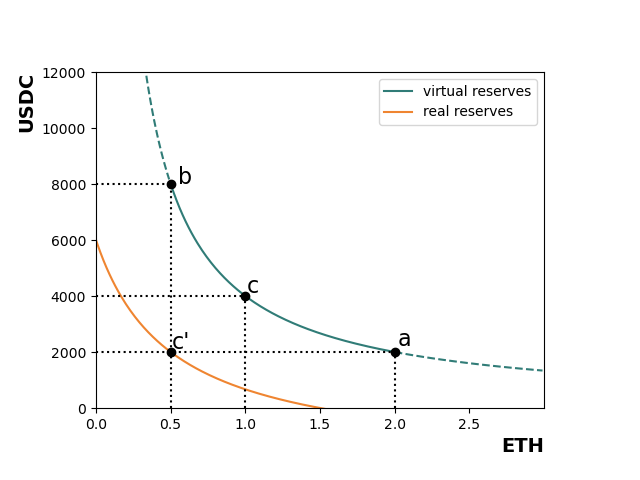
amm-demo

虚拟流动性曲线方程为 x⋅y=4000=kx \cdot y = 4000 = k，流动性 L=k=4000≈63.2455532L = \sqrt{k} = \sqrt{4000} \approx 63.2455532

a 点 ETH 价格 pa=yaxa=20002=1000p_a = \frac{y_a}{x_a} = \frac{2000}{2} = 1000

b 点 ETH 价格 pb=ybxb=80000.5=16000p_b = \frac{y_b}{x_b} = \frac{8000}{0.5} = 16000

在 C 点时，真实流动性 x = 0.5, y = 2000, 代入公式

(0.5+L16000)×(2000+L1000)=L2⇒L≈63.2455532(0.5 + \frac{L}{\sqrt{16000}}) \times (2000 + L\sqrt{1000}) = L^2 \Rightarrow L\approx 63.2455532

计算得到的 L 值与 k\sqrt{k} 一致

在合约中并不存储 xx 和 yy，仅通过 LL 和 P\sqrt{P}进行计算

TODO: [a, b] 区间提供流动性示例

价格​

由于在 v2 中同一个交易对的无穷价格区间在 v3 中被分成了多个更小的价格区间，而每个价格区间又是独立的函数曲线，独立的流动性，导致计算复杂。因此引入了新的坐标系 price-liquidity

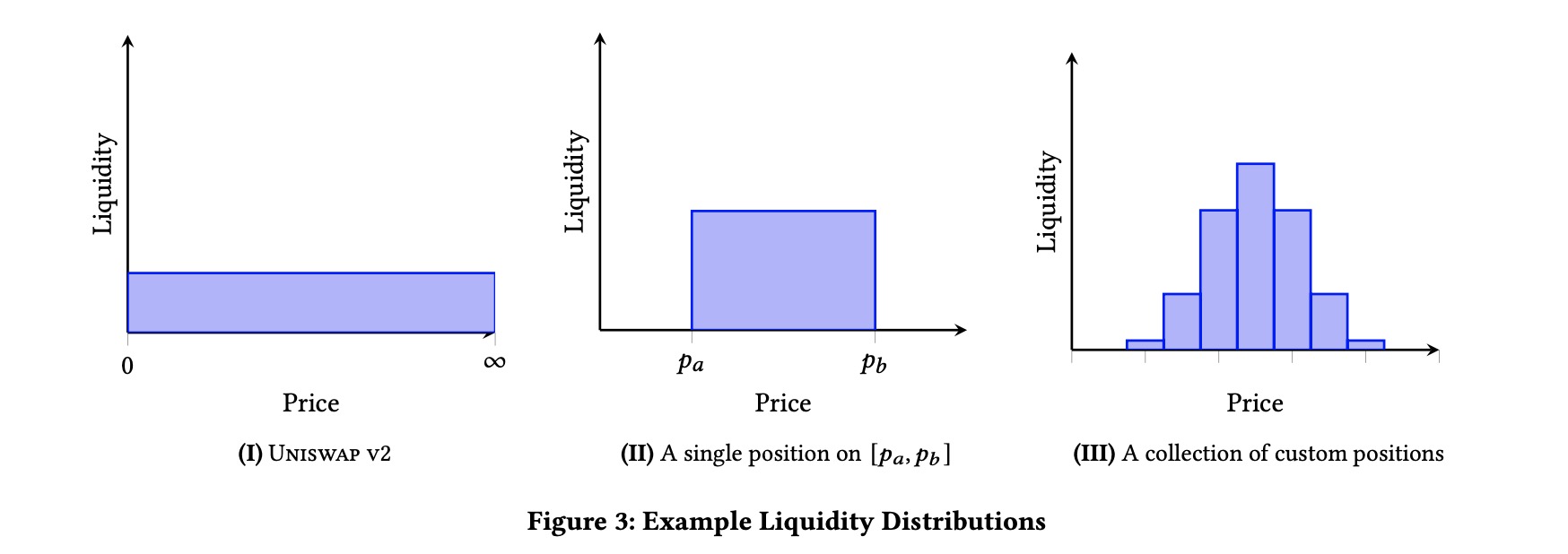
figure3

横坐标表示价格，纵坐标表示流动性。在实际的计算过程中要将 (x, y) 转换为 (price, liquidity), 转换过程满足下列公式

Δy=ΔPL\Delta_y = \Delta\sqrt{P}L

在 ticks 中整个价格区间由离散的、均匀分布的 tick 进行标定。每个 tick 有一个索引和对应的价格

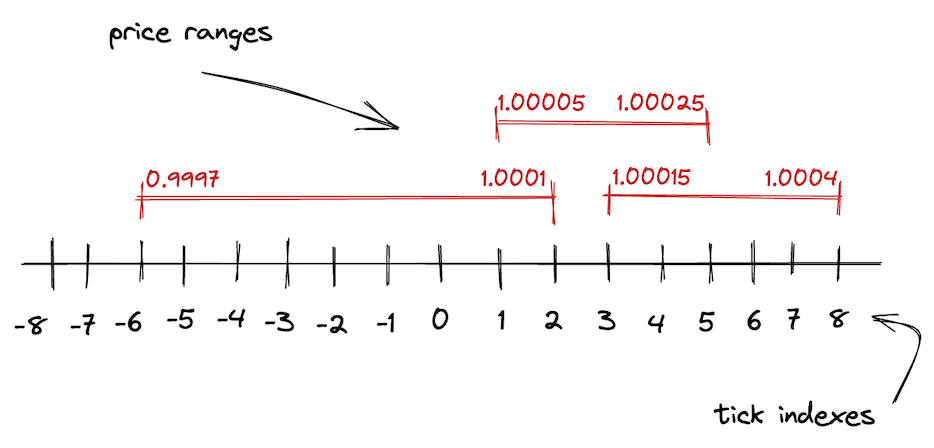
ticks_and_ranges

索引和价格存在下面的关系

p(i)=1.0001ii=log1.0001p(i)p(i) = 1.0001^i \\[2ex] i = log_{\sqrt{1.0001}}\sqrt{p(i)}

p(i)p(i) 即为 tick ii 对应的价格. 使用 1.0001 的幂次作为标定有一个很好的性质：两个相邻 tick 之间的差距为 0.01% 或者一个基点

示例​

提供流动性​

兑换​

最后于 更新