跳到主要内容

默克尔树简介

· 阅读需 6 分钟

基础​

在介绍默克尔树之前需要先了解什么是树。相信学过数据结构这门课程的同学并不陌生

树是一种数据结构，它是由n(n≥0)个有限节点组成一个具有层次关系的集合。如下图所示

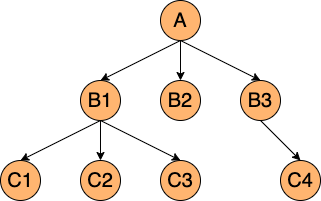
merkle-tree-001

可以看到每个节点下面包含若干个子节点，每个子节点又可以包含若干子孙节点。用代码简单描述为

class TreeNode {
  // 节点值
  value: string
  // 子节点数组
  childs: Array<TreeNode>

  constructor(value: string) {
    this.value = value
    this.childs = []
  }

  insert(node: TreeNode) {
    this.childs.push(node)
  }
}

const tree = new TreeNode('A')
const node1 = new TreeNode('B1')
const node2 = new TreeNode('B2')
const node3 = new TreeNode('B3')

// 添加子节点
tree.insert(node1)
tree.insert(node2)
tree.insert(node3)

而二叉树则是每个节点延伸的子节点数最多不超过两个。用代码描述为

class TreeNode {
  // 节点值
  value: string
  // 左节点
  left: TreeNode | null
  // 右节点
  right: TreeNode | null

  constructor(value: string, left?: TreeNode | null, right?: TreeNode | null) {
    this.value = value
    this.left = left ? left : null
    this.right = right ? right : null
  }
}

const left = new TreeNode('B1')
const right = new TreeNode('B2')

const tree = new TreeNode('A', left, right)

默克尔树则正是一种二叉树。不同的是每个节点的值存储的是数据的哈希值，而不是数据本身。所以默克尔树也叫做哈希树。

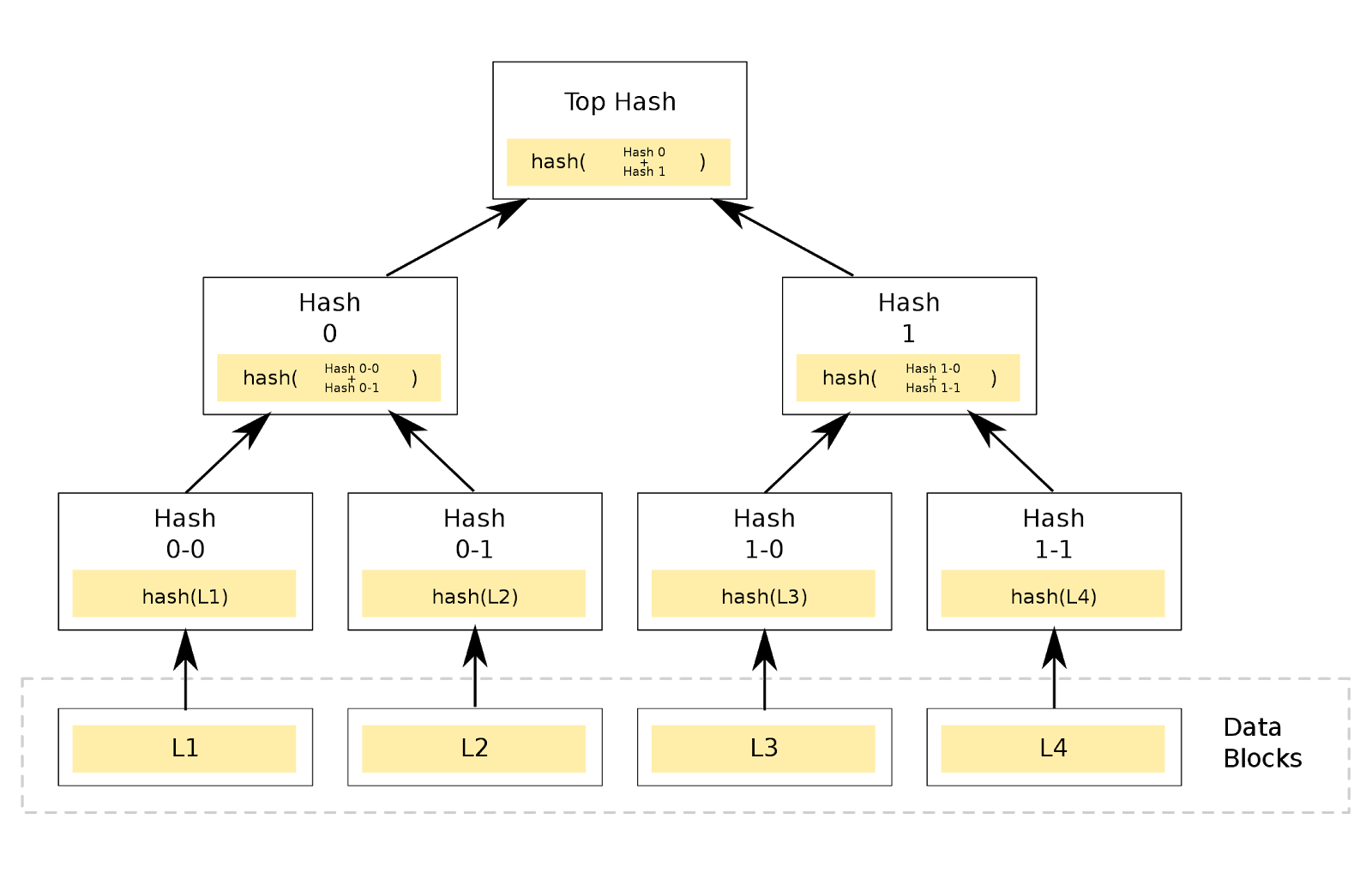
merkle-tree-002

从图中可以看出默克尔树的构造过程是自下而上的。首先生成最底层的节点，其值由原始数据经过 hash 运算得到，如数据 L1, 经过 hash 运算后得到 hash(L1) 作为节点值，而其父节点则是由 hash(L1)和 hash(L2) 再经过一次 hash 运算得到 hash(hash(L1), hash(L2)) 。如此循环，便生成了由原始数据 L1、L2、L3、L4 构造的默克尔树。

实现默克尔树​

节点类​

MerkleNode.ts

export default class MerkleNode {
  // 节点值
  value: string
  // 左节点
  left: MerkleNode | null
  // 右节点
  right: MerkleNode | null
  constructor(
    value: string,
    left?: MerkleNode | null,
    right?: MerkleNode | null
  ) {
    this.value = value
    this.left = left ? left : null
    this.right = right ? right : null
  }
}

默克尔树​

MerkleTree.ts

import MerkleNode from './MerkleNode'
// nodejs 内置库
import { createHash } from 'crypto'

// 将 data 进行 hash 运算
const hash = (data: string): string => {
  return createHash('sha256').update(data).digest('hex')
}

class MerkleTree {
  // 根节点
  root: MerkleNode
  // 节点数
  size: number

  constructor(root: MerkleNode, size: number) {
    this.root = root
    this.size = size
  }

  // 由原始数据 items 构造默克尔树
  static create(items: Array<string>) {
    const size = Math.ceil(Math.log2(items.length)) + 1
    // 构造原始数据的 hash 节点，即最底层节点
    const nodes = items.map((item) => new MerkleNode(hash(item)))
    const root = this.buildTree(nodes)
    return new MerkleTree(root, size)
  }

  // 由下往上向上逐层构造 merkel tree, 返回根节点
  static buildTree(nodes: Array<MerkleNode>): MerkleNode {
    const length = nodes.length

    // 已计算到根节点，直接返回
    if (length === 1) return nodes[0]

    // 存储当前层的节点
    const list: MerkleNode[] = []

    // 遍历节点，构造其父节点 - 父节点由其两个子节点经过 hash 运算得出
    for (let i = 0; i < nodes.length; i += 2) {
      const left = nodes[i]
      if (i + 1 >= length) {
        list.push(left)
        break
      }
      const right = nodes[i + 1]
      // 创建父节点
      const node = new MerkleNode(hash(left.value + right.value), left, right)
      list.push(node)
    }
    // 递归向上逐层构造父节点，直到根节点
    return this.buildTree(list)
  }
}

const tree = MerkleTree.create(['1', '2', '3', '4', '5', '6'])
console.log(tree.root.value)
console.log(tree.size)

以上只是默克尔树的简单实现，详细请参考 merkletreejs

应用​

假设有下面两颗树，tree2 是 tree1 的 0x02 数据变更为 0x10 后生成的树

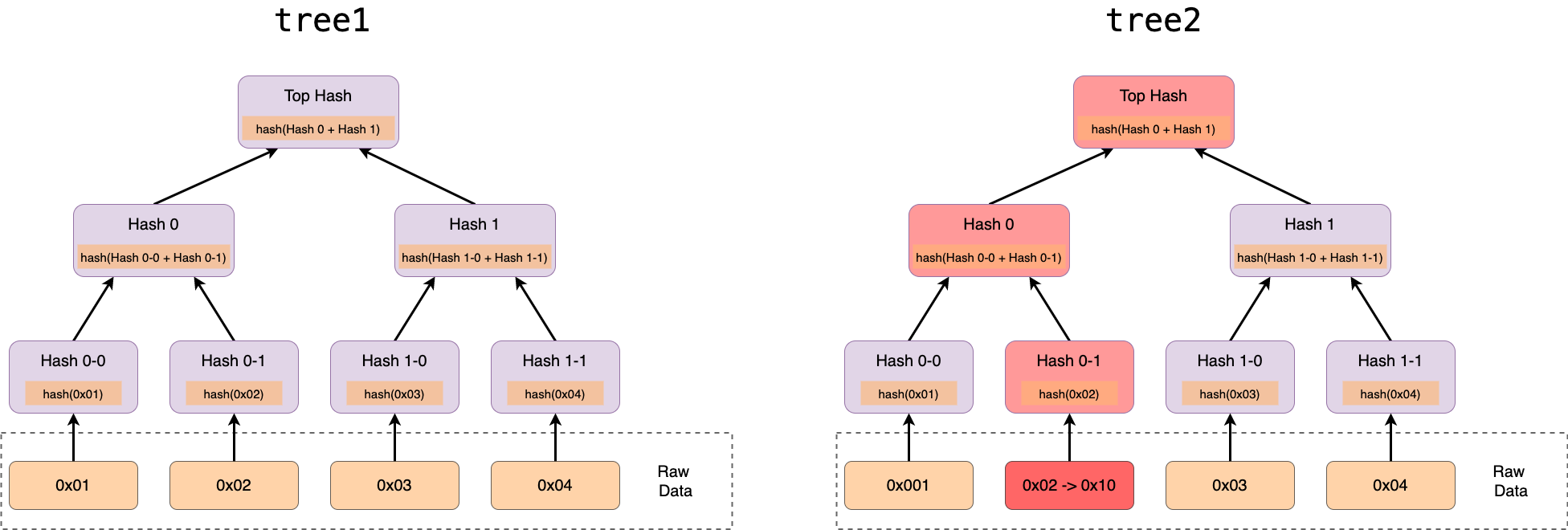
merkle-tree-003

校验分片数据的完整性​

当原始数据变化时，则由原始数据构造的默克尔树的根节点的值必然会变化。此时比较数据未发生变化前生成的默克尔树的根节点的值，则会大不相同。如上图中 tree1 和 tree2 的根节点的值就大不相同。

代码描述为

function isSameTree(tree1: MerkleTree, tree2: MerkleTree): bool {
  return tree1.root.value === tree2.root.value
}

快速定位修改的内容​

如上图中 tree1 中的原始数据0x02 变更为了 0x10 ，若想快速定位修改的内容，则只需要构造数据修改后的默克尔树 tree2。可以看到影响的节点有 Top Hash、Hash 0 、Hash 0-1 , 此时只需要从两棵树的根节点开始逐层对比，

  • 遇到相同的值则说明该节点及其子节点的值未发生变化，即可跳过。
  • 遇到不同的值，则继续对比其子节点, 直到最底层的节点

对比的时间复杂度为 O(log(n))O(log(n))