椭圆曲线加密算法

椭圆曲线定义

椭圆曲线加密算法（Elliptic curve cryptography）简称 ECC，是一种非对称加密算法。方程式为

$$y^2 = x^3 + ax +b，4a^3 + 27b^2 \neq 0$$

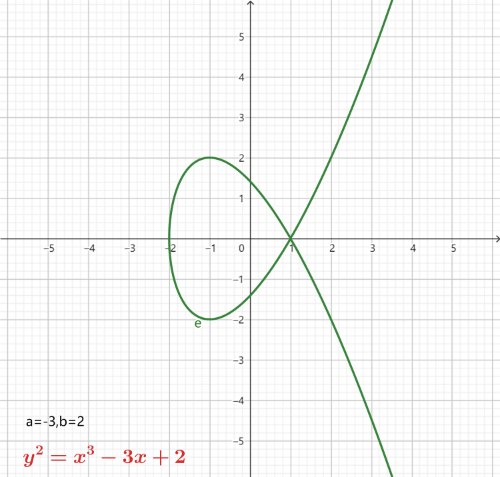
如下是不同的 $a$ 和 $b$ 取值绘制的椭圆曲线图

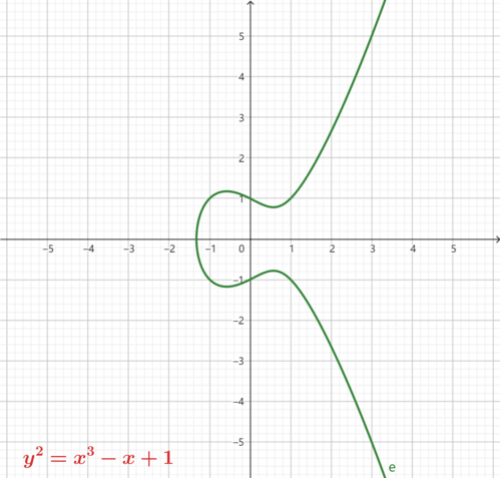
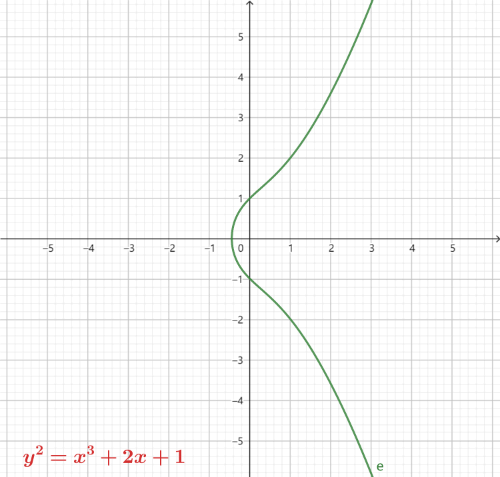
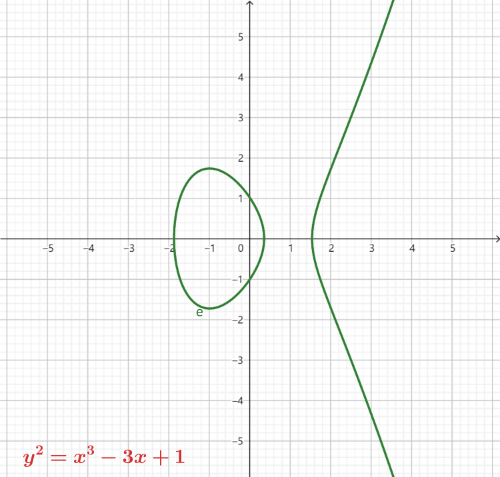
从图中可以看出，椭圆曲线是关于 x 轴对称的曲线。

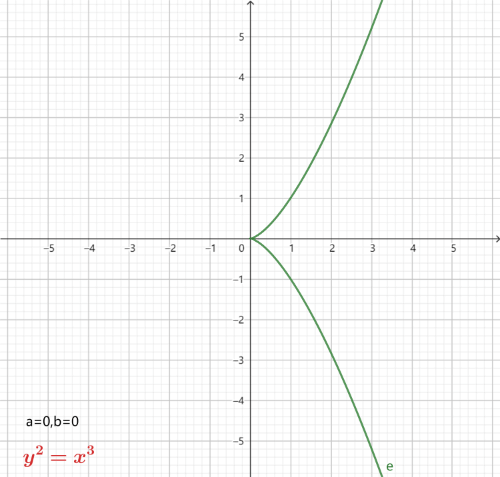
需要注意的是 $a$ 和 $b$ 须满足条件 $4a^3 + 27b^2 \neq 0$，这个条件确保了曲线的光滑，即曲线中不存在尖点，自相交点和孤立点，从而保证曲线上的点都有切线。

椭圆曲线的四则运算

椭圆曲线的四则运算不同于代数中的四则运算。其有自己的运算法则。

加法

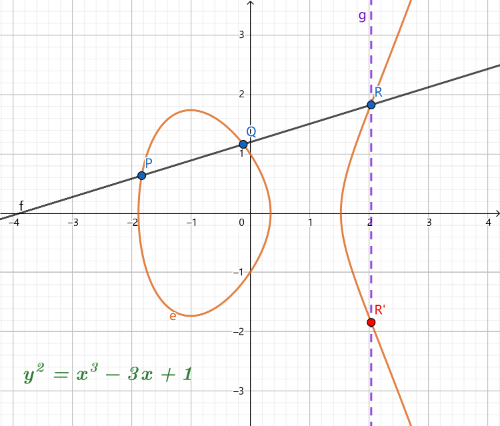
已知椭圆曲线上的点$P$和点$Q$，过这两点做直线，与椭圆曲线相交于第三个点$R$，做点$R$与 x 轴的对称点$R'$。这个$R'$点就时$P$和$Q$相加的结果，$P + Q = R’$

当 $P=Q$时，相当于过点 P 做曲线的切线，相交于点$R$，$R$ 关于 X 轴的对称点 $R'$ 就是相加得到的点。 $P + P = 2P = R'$

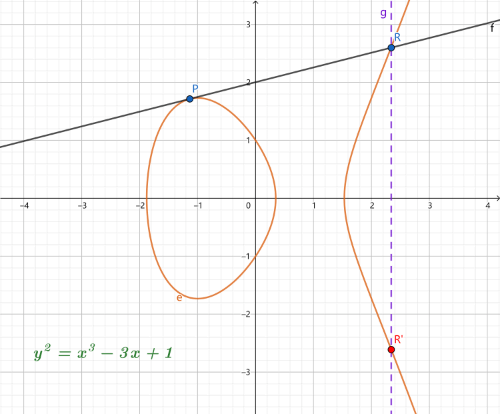
当$Q=-P$时，即$Q$点是$P$点在椭圆曲线上关于 X 轴的对称点，此时过这两点做直线。没有相交的第三个点。假设$P+Q = O$，则$P + Q = P + (-P) = O$

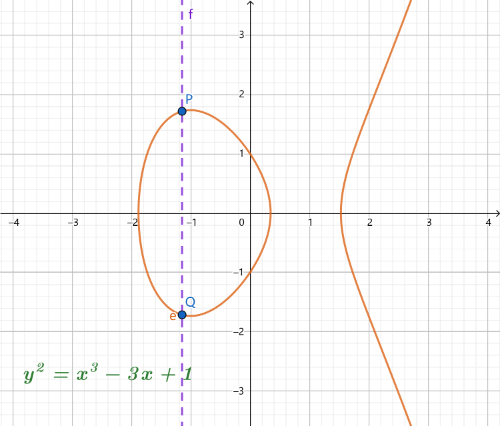
点$O$是一个无穷远点，也叫加法的单位元。曲线上任意点与单位元相加都等于其自身。 $P + O = P$

还有一种情况是 $P$ 和 $Q$ 连接的直线没有第三个交点的情况

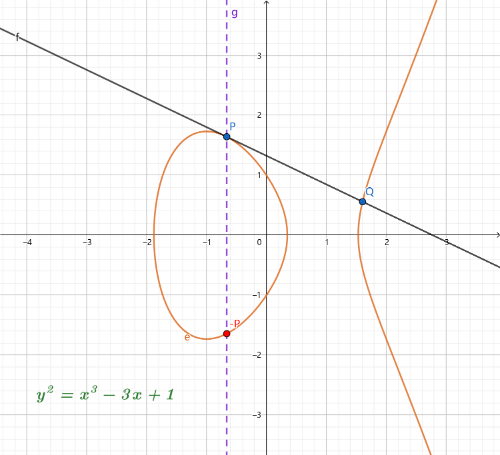
这种情况就是一条直线穿过 P 和 Q 与曲线相切，P 是切点，此时$P+Q = -P$, 同样如果 Q 是切点，则$P+Q=-Q$

减法

$P-Q$ 可以看成$P + (-Q)$

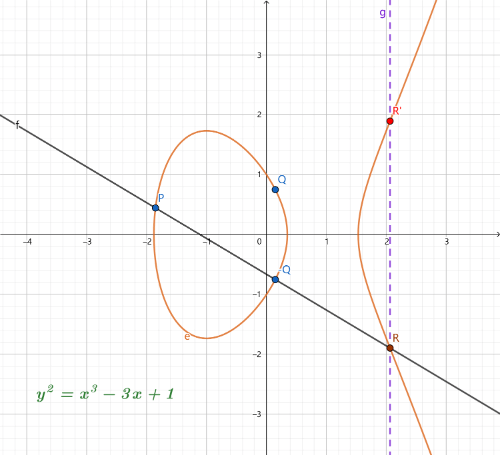
首先计算 $Q$ 关于 X 轴的对称点$-Q$，连接$P$和$-Q$相交于$R$, $R$关于 X 轴的对称点$R'$就是计算结果。

乘法

已知椭圆曲线上的点 P 和数值 n，求 nP，可以看成是 n 个 P 相加 例如 $P + P+ P$

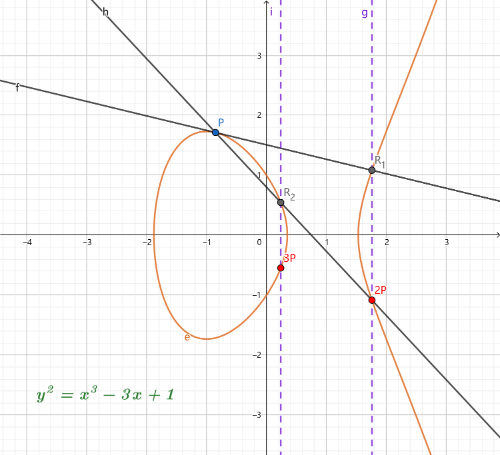
首先计算 $P + P$，过$P$点做切线与曲线相交于$R_1$，$R_1$ 关于 X 的对称点$2P$就是 $P+P$的结果，连接$2P$点和$p$点相交于$R_2$点，$R_2$关于 X 轴的对称点$3P$就是最终的计算结果

有限域椭圆曲线

上面所说的是在实数域上椭圆曲线，实数是具有连续性的，这种连续性并不适用于安全加密。因此需要把椭圆曲线变成离散的点，也就是定义在有限域上。

有限域是指有限个元素的集合,记做 $GF{(p)}$ 或 $𝔽_p$, $p$是素数，有$\{0,1,2,3...,p-1\}$共 p 个元素。如$𝔽_7=\{0, 1, 2, 3, 4, 5, 6\}$

在这个有限域中，椭圆曲线的运算都是基于取模运算的，也就是取余数

• 加法：$a + b = c \ mod \ p$
• 减法：$a-b = a + (-b) \ mod\ p$
• 乘法：$a * b = c \ mod \ p$
• 除法：$a \div b = a \times b ^ {-1}=c \ mod\ p$

在有限域$𝔽_p$上的椭圆曲线上满足:

• $y^2 = x^3 + ax + b$ 上的所有点的 $x$ 和 $y$ 坐标值是$𝔽_p$中的两个整数，因此有限域椭圆曲线图是一定数量的点形成的图
• $a$ 和 $b$ 是满足$4a^3 + 27b^2 \neq 0$且在$𝔽_p$中的两个整数

记作$E_p(a, b)$, 如：$E_{5}(1, 1): y^2 = x^3 +x + 1\ mod\ 5$

即对于某个$x$ 和 $y$ 的组合等式两边的结果对 5 取余是相等的，则认为该点是有效的

由于$x$ 和 $y$ 的取值是在有限域中整数，因此对于上式中有多个可组合的点：

• $x=0, y=1$, 左右两边对 5 取余结果都为 1，该点有效
• $x = 0, y = 2$, 左边对 5 取余结果为 4，右边对 5 取余结果为 1，两边不等，该点无效
• $x = 0, y = 4$, 左右两边对 5 取余结果都为 1，该点有效

如此遍历下去，便能确定最终的有效点为$(0, 1)\ (0,4)\ (2, 1)\ (2, 4), \ (3, 1)\ (3, 4)\ (4,2)\ (4,3)$

有限域椭圆曲线加法

假设有限域椭圆曲线$E_{127}(-1, 3): y^2=x^3 -x +3 \ mod \ 127$

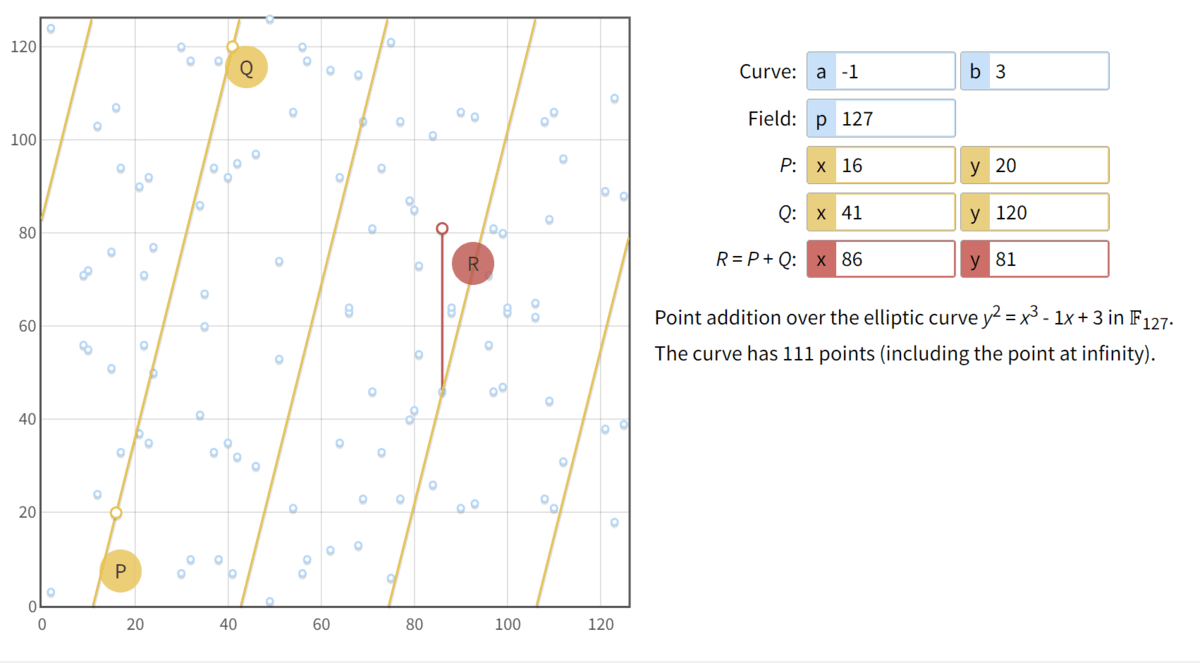
点$P=(16, 20)$, 点$Q =(41,120)$ 求 $P+Q$ 的坐标点$R'(x'， y')$

首先计算连接$P$ 和 $Q$ 直线的斜率$k = \frac {y_P - y_Q}{x_P - x_Q} \mod \ p= \frac {20-120}{16-41} \mod \ 127=4 \mod\ 127 = 4$

接着计算直线和曲线相交的第三个点的坐标$R(x, y)$：

$x_R = k^2 - x_P - x_Q \ mod\ p = 16-16-41 \ mod\ 127 = -41 \ mod\ 127 = 86$

$y_R=[y_P + k(x_R-x_P)] \ mod\ p = [20 + 4(86 - 16)]\ mod\ 127 = 300\ mod\ 127 = 46$

$R'$是$R$关于$x$轴的对称点，所以

$x_{R'} = x_R = 86， y_{R'}=-y_R \ mod\ p = -46 \mod \ 127 = 81$

所以 $P+Q = (86, 81)$

如果$P=Q$, 则斜率$k = \frac {3x_P^2 + a}{2y_P} \ mod\ p$

有限域椭圆曲线乘法

在实数域中的乘法定义为：$nP = P + P +\cdots + P$, 对$P$逐次累加计算。在有限域中同样可以这样计算

但在有限域中椭圆曲线中的乘法会存在一个循环，例如存在有限域椭圆曲线$E_{97}(2, 3): y^2=x^3+2x+3 \ mod\ 97$ 和点$P(3, 6)$

• $0P = 0$
• $1P = (3, 6)$
• $2P = P + P = (80, 10)$
• $3P=2P+P=(80, 87)$
• $4P=3P+P(3, 91)$
• $5P = 4P+P=0$
• $6P=5P+P=(3, 6)$
• $7P =6P+P =(80, 10)$
• $\cdots$

可视化查看网页

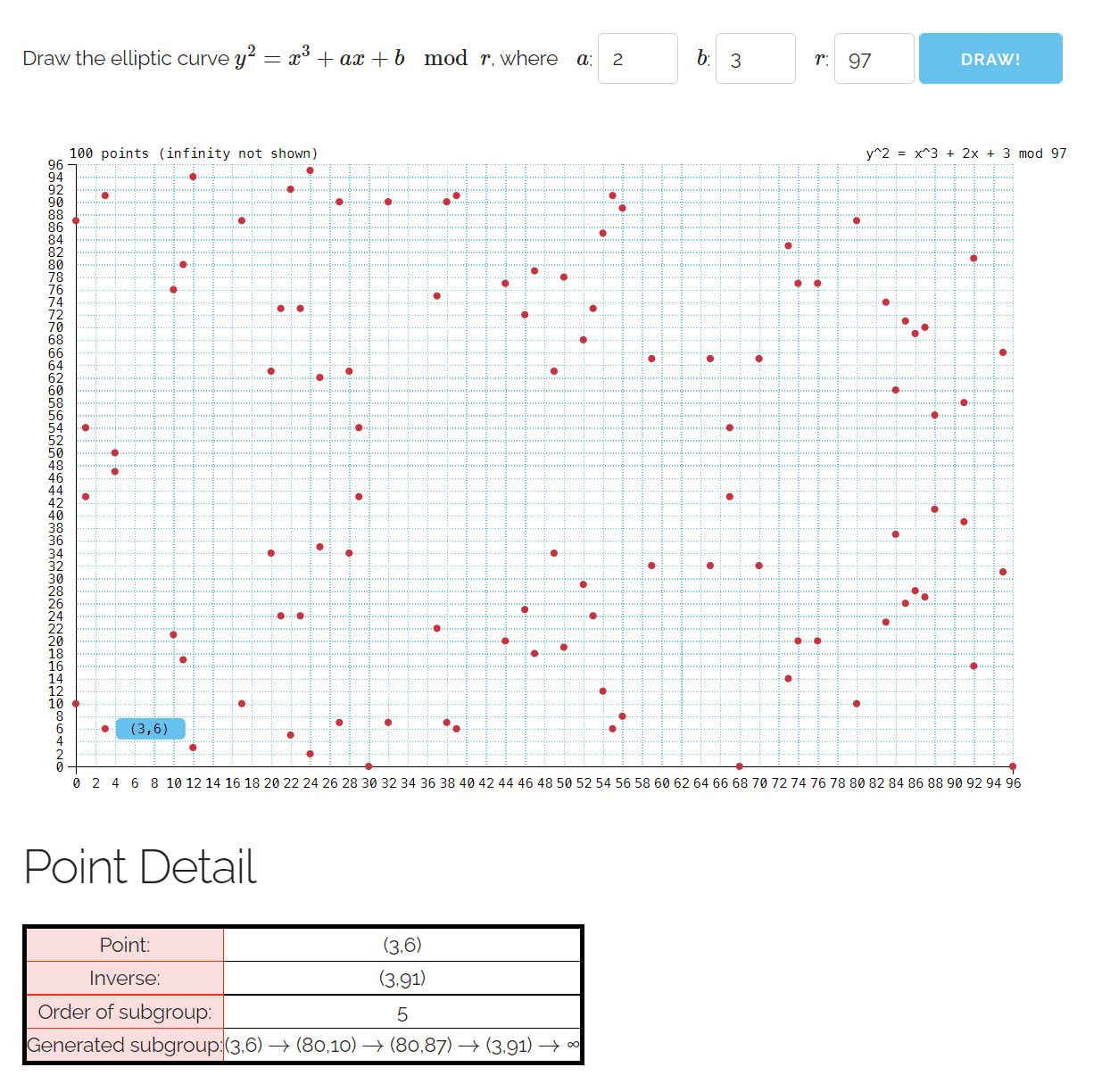
当点击点$P(3, 6)$ 时，可以看到循环次数为 5，以及循环计算得到的点集（称循环子群）。该点集的数量就叫做阶。即 5 是点$P(3,6)$的阶。

$P$的阶和椭圆曲线是有联系的，拉格朗日定理告诉我们，子群的阶是父群的阶的因子。换句话说，如果一个椭圆曲线包含 $N$ 个点，它的一个子群包含 $n$ 个点，那么 $n$ 是 $N$ 的因子

因此计算点$P$的阶就可以遵循下面的步骤：

• 计算椭圆曲线的阶$N$ （上面定义了阶是点集的数量，因此$N$ 就是有限域上椭圆曲线的有效点的数量）
• 找出$N$的所有因子
• 对每个因子计算$nP$
• 找到最小的且满足 $nP=0$ 的$n$, $n$ 就是子群的阶

例如对于椭圆曲线$E_{37}(-1, 3): y^2=x^3-x+3 \ mod\ 37$

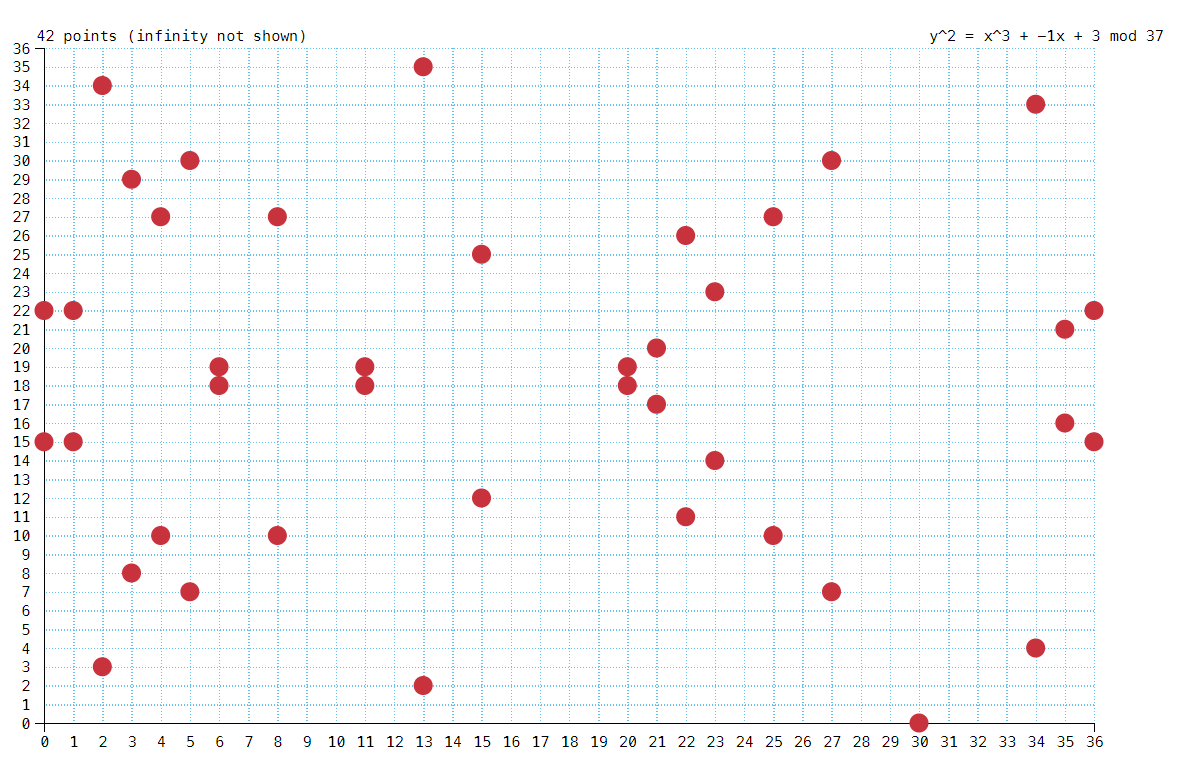
共有 42 个点，因此 $N = 42$。42 的因子有 $1,2,3,6,7,14,21,42$ 依次与点$P(2,3)$ 相乘

$1P\neq 0, 2P\neq0,\cdots,7P=0$, 因此$P$的阶是 7。

椭圆曲线加密算法

ECC

在椭圆曲线加密算法中，给定椭圆曲线$E$, 基点$G$，可以很容易算出$G$的阶$n$，然后在$\{1,\cdots,n-1\}$ 中随机选择一个整数$k$ 作为私钥，公钥$H=kG$

因此知道 $k$ 和 $G$ 可以很容易算出公钥 $H$ , 但如果知道$H$和$G$,要算出私钥$k$ 就很难了。这里涉及到了离散对数的问题

ECDH

ECDH 是椭圆曲线的笛福赫尔曼算法的变种，它其实不单单是一种加密算法，而是一种密钥协商协议， 也就是说 ECDH 定义了密钥怎么样在通信双方之间生成和交换。

假设现在有 A 和 B 想要通信，在ECDH 通信是下面这样的：

• A 选择了一条有限域上椭圆曲线$E_p(a,b)$ 并选择了一个基点$G$, 生成了自己的公钥和私钥。之后将自己的椭圆曲线$E_p(a,b)$、基点$G$ 和公钥传给 B。B 根据这些信息生成自己的公钥和私钥
  • A 的私钥记作$k_A$，公钥$H_A = k_AG$
  • B 的私钥记作$k_B$，公钥$H_B = k_BG$
• A 和 B 交换各自的公钥
• A 计算共享秘钥$S=k_AH_B$（使用自身的私钥和 B 的公钥）, B 计算共享秘钥$S=k_BH_A$（使用自身的私钥和 A 的公钥）, A 和 B 计算得到的$S$ 是相同的，因为$S=k_AH_B = k_A(k_BG) = k_B(k_AG)=k_BH_A$
• 使用共享秘钥来加密数据进行通信。

ECDSA

椭圆曲线签名算法（ECDSA）就是使用 ECC 对 DSA 数字签名算法的模拟，最终签名可得到两个值 r 和 s。验证签名只需要求解一个值，判断值是否与 r 相同，如果相同，则说明是有效签名。

已知椭圆曲线$E_p(a, b)$ 、基点$G$、 $G$的阶数$n$，要发送的消息的哈希$h=hash(message)$，经过计算后 h 会是一个整数

A 首先生成自己的公钥和私钥，即从$\{1,\cdots,n-1\}$随机选择一个数$k_A$作为私钥，公钥 $H_A=k_AG$

A 生成签名过程如下

• 在$\{1,\cdots,n-1\}$ 中选择一个随机数$k$
• 计算 $P(x, y)=kG$
• 计算$r = x_P\ mod\ n$ （$x_P$为$P$点的$x$坐标），若$r=0$, 则重新选择一个$k$ 并重新计算
• 计算$s=k^{-1} (h+rk_A) \ mod\ n$ （$k_A$是 A 的私钥，$k^{-1}$ 是$k$的乘法逆元， h 是要发送消息的哈希），若$s=0$ ,则重新选择一个$k$并重新计算

为了验证签名，我们需要将 A 的公钥 $H_A$ ，消息哈希$h$，签名信息$(r,s)$，发送给 B

B 验证签名过程如下:

• 计算$u_1 = s^{-1}h \ mod \ n$
• 计算$u_2 = s^{-1}r \ mod \ n$
• 计算$P = u_1G + u_2H_A$, 当 $r = x_P \ mod \ n$ （x_P为$$P的$x$坐标），则验证成功

$P = u_1G + u_2H_A = u_1G + u_2k_AG = (u_1 + u_2k_A)G = (s^{-1}h + s^{-1}rk_A)G = (h+rk_A)s^{-1}G$

由于$s=k^{-1} (h+rk_A) \ mod\ n$

所以$P=(h+rk_A) \frac {k}{h+rk_A}G = kG$

ECDSA 实践：

假设现在有 A 和 B 需要通信

已知信息

• 椭圆曲线$E_{29}(4,20): y^2=x^3+4x+20 \ mod\ 29$
• 基点$G=(2, 6)$， $G$的阶$n=37$
• 消息$h=Hash(message) = 88$

A 签名

• 在$[1,36]$随机选择一个整数 7 作为私钥，则公钥$H=kG=7(2,6)=(3,28)$
• 在$[1, 36]$随机生成一个整数$k=11$
• 计算$P=kG = 11(2, 6) = (16,2)$
• 计算$r=x_P\ mod\ n = 16 \ mod\ 37 = 16$
• 计算$s = k^{-1} (h+rk_A) \ mod\ n = k^{-1}(88+16*7) \ mod\ n=200k^{-1} \ mod \ 37 = 200 * 27 \ mod\ 37 = 35$
• 发送$(r, s)$ 、A 的公钥$H_A$、消息$h$ 给 B

B 验证签名

• 计算$u_1=s^{-1}h \ mod \ n = 18 * 88 \ mod\ 37=30$
• 计算$u_2 = s^{-1}r \ mod \ n = 18 * 16\ mod\ 37 = 29$
• 计算$R = u_1G + u_2H_A = 30(2, 8) + 29(3, 28) = (16, 2)$
• 计算 $x_R \ mod\ n = 16 \ mod\ 37 = 16 = r$, 说明签名合法

secp256k1

secp256k1 是一条特定的椭圆曲线，椭圆曲线方程中 a =0, b = 7，故方程为$y^2 = x^3 + 7$。曲线图如下：

有限域为$GF{(p)}$

$p=2^{256} - 2^{32}-2^{9}-2^8-2^7-2^6-2^4-1$

= 0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f

基点

G=(0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798, 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8)

$G$的阶

$n = 2^{256}-4324203865659656852420866394968145599$

=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141

从[1, n-1] 随机取一个数$k$作为私钥，则公钥$H=kG$

总结：

• ecc: 如何生成公私钥
• ecdh：通信双方如何生成相同的加密秘钥
• ecdsa：对通信的消息如何签名才能确保消息没有被篡改
• secp256k1：特定的椭圆曲线

参考

• elliptic-curve-cryptography-a-gentle-introduction
• elliptic-curve-cryptography-finite-fields-and-discrete-logarithms
• elliptic-curve-cryptography-ecdh-and-ecdsa
• modk-add
• 大白话椭圆曲线加密算法